Jednowymiarowa studnia potencjału – zjawisko tunelowe

Jednowymiarowa studnia potencjału to jeden z najprostszych modeli studni potencjału. Zagadnienie cząstki w studni potencjału jest jednym z najprostszych przykładów z tematyki fizyki kwantowej. Cząstka umieszczona we wnętrzu studni potencjału może poruszać się w jednym wymiarze przestrzennym, pomiędzy barierami potencjału.

Na rysunku poniżej przedstawiony został przebieg potencjału, nazywany jest on nieskończenie głęboką studnią potencjału.

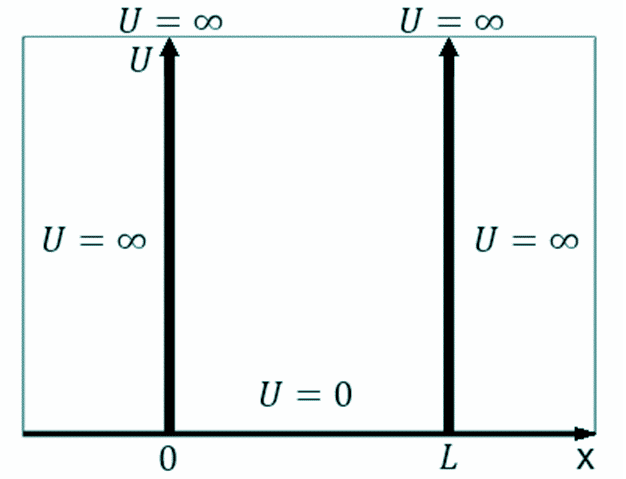
Używane do opisu słowo „studnia” związane jest z analogią do realnej studni ze względu na brak możliwości opuszczenia danego obszaru przez cząstkę.

W rozważanym przypadku rozpatrywaną cząstką jest elektron, który nie może opuścić studni potencjału ze względu na działające na niego siły o nieskończenie dużej wartości. Zmienia ona zwrot prędkości elektronu na przeciwny co skutkuje uwięzieniem go w studni.

Podczas pobytu elektronu wewnątrz nieskończenie głębokiej studni potencjału wartość jego energii potencjalnej jest równa potencjałowi w obszarze, w którym się znajduje tym samym przyjmuje wartość zero. [1, 2].

Ruch cząstki w jednowymiarowej studni potencjału może być analizowany na dwa sposoby. Pierwszy z nich zakłada użycie założeń fizyki klasycznej, w tym przypadku cząstka poruszająca się ruchem jednostajnym prostoliniowym wzdłuż osi X, odbijać się będzie od ścian studni pod kątem równym kątowi padania [1].

Na rysunku 2 przedstawiona została sytuacja, w której elektron w postaci punktu materialnego zbliża się do bariery potencjału. Nie pokona on jednak bariery, ponieważ jego energia jest zdecydowanie mniejsza od wysokości bariery [1, 3]

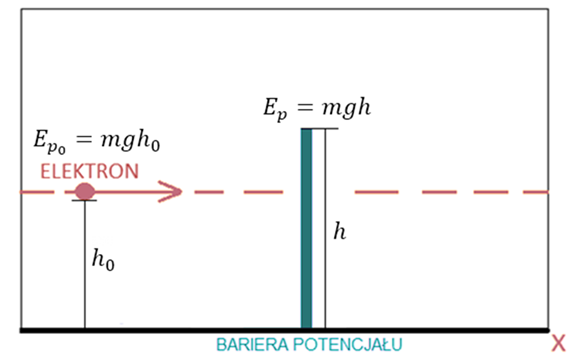
Drugi ze sposobów analizy zachowania elektronu zakłada zastosowanie założeń mechaniki kwantowej. Przewidują one istnienie efektu tunelowania, który polega na przenikaniu cząstek przez barierę potencjału. Takie zjawisko nazywane jest tunelowym, zachodzi ono w przypadku przejścia cząstki przez barierę potencjału o wysokości większej niż energia cząstki. W przypadku pokazanym powyżej równoległy do osi X tor lotu elektronu zostałby zachowany tylko i wyłącznie w przypadku zajścia efektu tunelowego. W przykładzie rozważany jest jeden elektron, przykład z użyciem większej ich liczby pojawi się w dalszej części skryptu.

Taka cząstka przebywać będzie przez chwilę w obszarze zabronionym przez zasadę zachowania energii co spowoduje, że złamane zostaną przez nią założenia fizyki klasycznej. Poza samym odbijaniem się cząsteczki wewnątrz studni od jej ścian, które musiałoby zachodzić bezstratnie, żeby ruch ten był trwały, istnieje też opisana wyżej sprzeczność z zasadą zachowania energii co czyni ten przykład rozwiązywalnym tylko przy zastosowaniu zasad mechaniki kwantowej. Według założeń mechaniki kwantowej, cząsteczki mają naturę korpuskularno-falową, czyli posiadać mogą własności odpowiadające zarówno cząsteczką jak i falą.

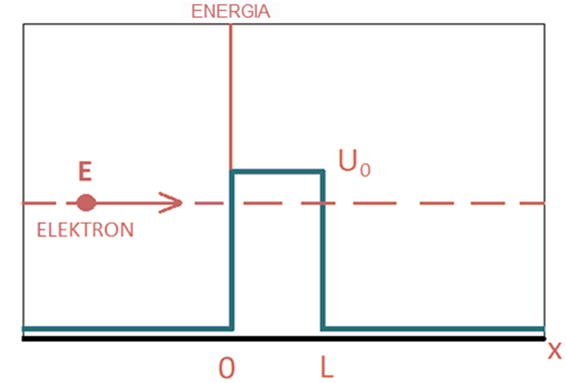
Na rysunku 3 przedstawiona została sytuacja, w której elektron w postaci fali porusza się w kierunku bariery potencjału wzdłuż do osi X. Posiada on energię całkowitą E, natomiast bariera potencjału posiada wysokość U₀ i szerokość L. Siły działające na wspomniany elektron powodują, że jego energia potencjalna jest równa zeru wszędzie poza obszarem  a energia w całym tym obszarze przybiera wartość U₀ . Obszar ten nazywany jest barierą energii potencjalnej.

Rozważanie tej sytuacji w ramach założeń fizyki klasycznej w przypadku, gdy:

E < U₀

skutkować będzie odbiciem elektronu od bariery co spowoduje zmianę zwrotu na przeciwny, kierunek nie zostanie zmieniony, odbicie nastąpi z kątem równym kątowi padania.

Założenia mechaniki kwantowej, mówiące o falowej naturze materii pozwalają na zajście efektu tunelowania, czyli istnieje tym samym skończone prawdopodobieństwo, że elektron przeniknie przez barierę potencjału i zachowa swój początkowy kierunek i zwrot.

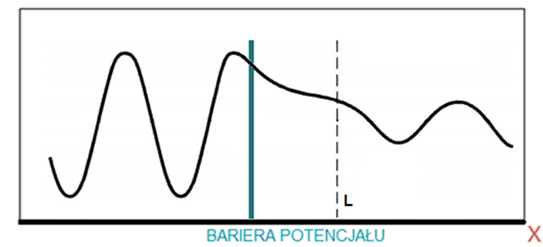
Amplituda takiej fali maleć będzie w sposób wykładniczy wraz z głębokością przenikania. Jest to zobrazowane na rysunku 4. Warto jednak zaznaczyć, że jest to rysunek poglądowy a rzeczywisty przebieg amplitudy fali po prawej stronie od bariery potencjału jest niemożliwy do narysowania w tej skali.

---